XOR連結リスト

連結リストは基本的なデータ構造の1つです。
連結リストのなかでも代表的な構造「単方向リスト」と「双方向リスト」を比較すると
　・単方向リストはメモリ使用量を抑えられるが逆方向に辿れない
　・双方向リストは逆方向に辿れるがメモリ使用量が増える
という特徴を持っています。
ここでは、メモリ使用量は単方向リストと同じで、かつ逆方向に辿れるいいとこどりな構造「XOR連結リスト」を説明します。　

単方向リスト
双方向リスト
XOR連結リスト
XOR連結リストの性能
ソースコード

単方向リスト

まず単方向リストのデータ構造を説明します。
連結リストでは各データをノードで表します。単方向リストの場合、さらに次のノードへのポインタを持ちます。

struct Node
{
  T data;
  Node* next;
};

図で表すと以下のようになります。

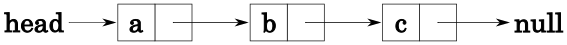
双方向リスト

続いて、双方向リストです。
双方向リストの場合、ノードにはデータ値、前のノードへのポインタ、次のノードへのポインタを持ちます。

struct Node
{
  T data;
  Node* prev;
  Node* next;
};

図で表すと以下のようになります。

単方向リストのNode構造体と比べると、前のノードへのポインタprevが追加されています。このメンバにより、前のノードに辿れるようになりますが、メモリ使用量が増えることになります。

XOR連結リスト

次にいいとこどりのXOR連結リストです。

struct Node
{
  T data;
  Node* diff;
};

ノードにはデータ値とポインタ差分を表すdiffを持ちます。

diffには前後のポインタの排他的論理和（XOR）を保持します。
例えば、bの値を持つノードでは、前ノードのポインタpaと次ノードのポインタpcの排他的論理和pa\(\oplus\)pcを持ちます。

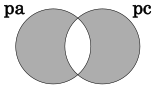
次ノードに辿るときは前ノードpaとの排他的論理和を計算することで次ノードpcを求めます。

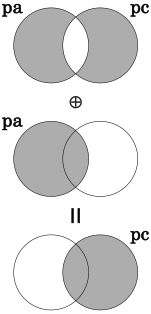
逆に、前ノードに辿るときは次ノードpcとの排他的論理和を計算することで前ノードpaを求めます。

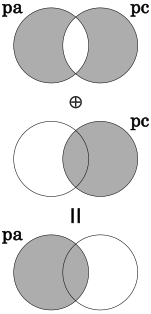
この仕組みにより、1つのアドレスのメモリ使用量で前後ノードへの移動を実現しています。

XOR連結リストの性能

XOR連結リストの良いところを説明してきましたが、気になるのはその処理時間です。
ここでは、100,000要素のリストを辿る処理を100,000回行った処理時間を計測します。
Visual Studio 2017を使用し、最適化オプションは無効(/Od)にしてあります。
結果は以下のとおりです。（単位：秒）

	単方向リスト	双方向リスト	XOR連結リスト
Forward	27.179	25.809	33.092
Backward	ー	29.172	34.919

　・単方向リストForwardが双方向リストForwardより遅い（ほぼ同等のはず）
　・BackwardがForwardより遅い（ほぼ同等のはず）
など、不可解な点はありますが、双方向リストとXOR連結リストの比較では、
　・XOR連結リストForwardは双方向リストForwardの1.28倍
　・XOR連結リストBackwardは双方向リストBackwardの1.20倍
となりました。
この速度低下が許容できるのであれば、XOR連結リストを検討しても良いかもしれませんね。

ソースコード

単方向リスト、双方向リスト、XOR連結リストのソースコードを以下に掲載します。

#pragma once

#include <cassert>

template<typename T>
class SinglyLinkedList
{
public:
  SinglyLinkedList()
  {
    m_head = new Node;
    m_head->next = 0;
  }

  virtual ~SinglyLinkedList()
  {
    Clear();
    delete m_head;
  }

  virtual void Insert(int pos, const T& data)
  {
    Node* cur_node = m_head;
    for (int i = 0; i < pos; ++i)
    {
      cur_node = cur_node->next;

      if (cur_node == 0)
      {
        assert(0);  // 挿入位置よりリストのサイズが小さい
        return;
      }
    }

    Node* prev_node = cur_node;
    Node* next_node = cur_node->next;

    Node* new_node = new Node;
    new_node->data = data;
    new_node->next = 0;

    new_node->next = next_node;
    prev_node->next = new_node;
  }

  virtual void Delete(int pos)
  {
    Node* cur_node = m_head;
    for (int i = 0; i < pos; ++i)
    {
      cur_node = cur_node->next;

      if (cur_node == 0)
      {
        assert(0);  // 削除位置よりリストのサイズが小さい
        return;
      }
    }

    Node* prev_node = cur_node;
    cur_node = cur_node->next;

    if (cur_node == 0)
    {
      assert(0);  // 削除位置よりリストのサイズが小さい
      return;
    }

    prev_node->next = cur_node->next;

    delete cur_node;
  }

  virtual int Size() const
  {
    Node* cur_node = m_head->next;
    int count = 0;
    while (cur_node != 0)
    {
      ++count;
      cur_node = cur_node->next;
    }
    return count;
  }

  virtual void Clear()
  {
    Node* cur_node = m_head->next;
    while (cur_node != 0)
    {
      Node* next_node = cur_node->next;
      delete cur_node;
      cur_node = next_node;
    }
    m_head->next = 0;
  }

  virtual bool IsEmpty() const
  {
    return (m_head->next == 0);
  }

  virtual void First()
  {
    m_cur = m_head->next;
  }

  virtual void Next()
  {
    m_cur = m_cur->next;
  }

  virtual bool IsDone() const
  {
    return (m_cur == 0);
  }

  virtual T Item() const
  {
    return m_cur->data;
  }

private:
  struct Node
  {
    T data;
    Node* next;
  };

private:
  Node* m_head;
  Node* m_cur;
};

#pragma once

#include <cassert>

template<typename T>
class DoublyLinkedList
{
public:
  DoublyLinkedList()
    : m_head(new Node)
    , m_tail(new Node)
  {
    m_head->prev = 0;
    m_head->next = m_tail;
    m_tail->prev = m_head;
    m_tail->next = 0;
  }

  virtual ~DoublyLinkedList()
  {
    Clear();
    delete m_head;
    delete m_tail;
  }

  virtual void Insert(int pos, const T& data)
  {
    First();
    for (int i = 0; i < pos; ++i)
    {
      if (IsDone())
      {
        assert(0);  // 挿入位置よりリストのサイズが小さい
        return;
      }

      Next();
    }
    Node* prev_node = m_cur->prev;
    Node* next_node = m_cur;

    Node* new_node = new Node;
    new_node->data = data;
    new_node->prev = 0;
    new_node->next = 0;

    new_node->next = next_node;
    new_node->prev = prev_node;
    prev_node->next = new_node;
    next_node->prev = new_node;
  }

  virtual void Delete(int pos)
  {
    First();
    for (int i = 0; i < pos; ++i)
    {
      Next();

      if (IsDone())
      {
        assert(0);  // 削除位置よりリストのサイズが小さい
        return;
      }
    }

    Node* prev_node = m_cur->prev;
    Node* next_node = m_cur->next;

    prev_node->next = next_node;
    next_node->prev = prev_node;

    delete m_cur;
  }

  virtual int Size() const
  {
    Node* cur_node = m_head->next;
    int count = 0;
    while (cur_node != m_tail)
    {
      ++count;
      cur_node = cur_node->next;
    }
    return count;
  }

  virtual void Clear()
  {
    Node* cur_node = m_head->next;
    while (cur_node != m_tail)
    {
      Node* next_node = cur_node->next;
      delete cur_node;
      cur_node = next_node;
    }
    m_head->next = m_tail;
    m_tail->prev = m_head;
  }

  virtual bool IsEmpty() const
  {
    return (m_head->next == m_tail);
  }

  virtual void First()
  {
    m_cur = m_head->next;
  }

  virtual void Last()
  {
    m_cur = m_tail->prev;
  }

  virtual void Prev()
  {
    m_cur = m_cur->prev;
  }

  virtual void Next()
  {
    m_cur = m_cur->next;
  }

  virtual bool IsDone() const
  {
    return (m_cur == m_head || m_cur == m_tail);
  }

  virtual T Item() const
  {
    return m_cur->data;
  }

private:
  struct Node
  {
    T data;
    Node* prev;
    Node* next;
  };

private:
  Node* m_head;
  Node* m_tail;
  Node* m_cur;
};

#pragma once

#include <cassert>

template<typename T>
class XORLinkedList
{
public:
  XORLinkedList()
    : m_head(new Node)
    , m_tail(new Node)
  {
    m_head->diff = m_tail;
    m_tail->diff = m_head;
  }

  virtual ~XORLinkedList()
  {
    Clear();
    delete m_head;
    delete m_tail;
  }

  virtual void Insert(int pos, const T& data)
  {
    First();
    for (int i = 0; i < pos; ++i)
    {
      if (IsDone())
      {
        assert(0);  // 挿入位置よりリストのサイズが小さい
        return;
      }

      Next();
    }

    Node* prev_node = m_prev;
    Node* next_node = m_cur;

    Node* new_node = new Node;
    new_node->data = data;
    new_node->diff = XOR(prev_node, next_node);

    prev_node->diff = XOR(prev_node->diff, next_node);
    prev_node->diff = XOR(prev_node->diff, new_node);
    next_node->diff = XOR(next_node->diff, prev_node);
    next_node->diff = XOR(next_node->diff, new_node);
  }

  virtual void Delete(int pos)
  {
    First();
    for (int i = 0; i < pos; ++i)
    {
      Next();

      if (IsDone())
      {
        assert(0);  // 削除位置よりリストのサイズが小さい
        return;
      }
    }

    Node* prev_node = m_prev;
    Node* cur_node = m_cur;
    Next();
    Node* next_node = m_cur;

    prev_node->diff = XOR(prev_node->diff, cur_node);
    prev_node->diff = XOR(prev_node->diff, next_node);
    next_node->diff = XOR(next_node->diff, cur_node);
    next_node->diff = XOR(next_node->diff, prev_node);

    delete cur_node;
  }

  virtual int Size() const
  {
    Node* cur_node = m_head->diff;
    Node* prev_node = m_head;
    int count = 0;
    while (cur_node != m_tail)
    {
      ++count;
      Node* next_node = XOR(cur_node->diff, prev_node);
      prev_node = cur_node;
      cur_node = next_node;
    }
    return count;
  }

  virtual void Clear()
  {
    First();
    while (!IsDone())
    {
      Node* prev = m_cur;
      Next();
      delete prev;
    }
    m_head->diff = m_tail;
    m_tail->diff = m_head;
  }

  virtual bool IsEmpty() const
  {
    return (m_head->diff == m_tail);
  }

  virtual void First()
  {
    m_cur = m_head->diff;
    m_prev = m_head;
  }

  virtual void Last()
  {
    m_cur = m_tail->diff;
    m_next = m_tail;
  }

  virtual void Prev()
  {
    if (m_next == 0)
    {
      assert(0);  // 順方向走査中
      return;
    }
    Node* prev = XOR(m_cur->diff, m_next);
    m_next = m_cur;
    m_cur = prev;
  }

  virtual void Next()
  {
    if (m_prev == 0)
    {
      assert(0);  // 逆方向走査中
      return;
    }
    Node* next = XOR(m_cur->diff, m_prev);
    m_prev = m_cur;
    m_cur = next;
  }

  virtual bool IsDone() const
  {
    return (m_cur == m_head || m_cur == m_tail);
  }

  virtual T Item() const
  {
    return m_cur->data;
  }

private:
  struct Node
  {
    T data;
    Node* diff;
  };

private:
  Node* XOR(Node* a, Node* b) const
  {
    return reinterpret_cast<Node*>(reinterpret_cast<uintptr_t>(a) ^ reinterpret_cast<uintptr_t>(b));
  }

private:
  Node* m_head;
  Node* m_tail;
  Node* m_cur;
  Node* m_prev;
  Node* m_next;
};